[Author's note: This article is intended for a general audience of Texas Longhorn breeders, rather than a technical audience. However, some scientific jargon is unavoidable, so if any of the terms are unfamiliar, please see the Glossary. If you have suggestions for other terms that should be in the glossary, please e-mail me. If the article is not clear to you, then I want to know where and why, so that I can fix it.—DMH]

Most traits of interest in Texas Longhorns are controlled by many different genetic loci, and many of these traits are also influenced by the environment in which the animal was raised and now lives. These traits typically are expressed along a continuum, rather than as a series of discrete states. For instance, the amount of milk produced by a cow clearly is influenced by her genetics, but it is also influenced by environmental factors (such as how much and what kind of food is available to the cow). Moreover, cows vary along a continuum in how much milk they produce. Such traits are called quantitative traits.

Quantitative traits differ considerably in the proportion of the variation in the trait that is the result of genetic factors (and therefore, also in the proportion of the variation that is the result of environmental factors). The variation due to a genetic basis is usually represented by the symbol V_g, and the total variation in the trait (variation in phenotype) is represented by the symbol V_p(note that this includes variation due to genetic influences, environmental factors, and possibly random variation). The ratio of V_g/V_p is called the heritability of the trait (in other words, it is the proportion of the total phenotypic variation that has a genetic basis). Heritability (V_g/V_p) is also symbolized h², especially when we are primarily considering the additive effects of genes (see the Glossary for the distinction between narrow-sense heritability and broad-sense heritability). Heritability values can range from 0 to 1. A heritability of 0 means that the observed variation does not have a genetic basis, whereas a heritability near 1 means that the observed variation in the trait is largely explained by genetic makeup.

Why should Texas Longhorn breeders care about the heritability of a trait? Because in selecting for favorable traits, heritability is one of the two factors that influence how much (and how quickly) a quantitative trait can be expected to change in a breeding program.The breeder's equation describes the relationship between a response to selection for a given trait, the heritability of that trait, and the intensity of the selection applied to the herd. The breeder's equation may be written as

R = h² S

where

R = the response to selection (or in other words, the change in the mean of the trait in a population after selection)
h² = heritability (as discussed above), and
S = the selection coefficient (or in other words, the difference in the mean of the trait for the original population and mean of the trait for the population of individuals selected for breeding)

Perhaps it is easiest to understand the meaning of R and S through an example. Imagine that we wish to select for long horns in a herd of Texas Longhorns (that probably doesn't take too much imagination!). Let's assume that we start with a herd of 62 cows that have tip-to-tip horn measurements that range from 40" to 64". Let's further assume that these cows are randomly drawn from the same breeding program, so that horn length is roughly normally distributed around the population mean of 52" for tip-to-tip measurement of the horns (all measurements are assumed to be taken at the same age...say 5 years). If we wish to select for long horns, then obviously we want to breed the longest-horned individuals from this population. This could involve breeding all the individuals above the mean, or just the individuals with >60" of horn, or some other strategy. If we select a minimum horn-length for the cows we will use, this kind of selection is known as truncation selection, and the more severe the truncation, the stronger is the selection. The selection coefficient (S ) is a measure of the strength of selection, and is simply the difference in the mean of the trait for the original population and mean of the trait for the population of individuals selected for breeding. If we only use the cows (and bulls) with 60" or more of horn in our breeding program, then this example may be illustrated graphically as follows:

In this case, the selection coefficient (S ) is 61" – 52" = 9". Since all the cows (and bulls) we used in this breeding program had 60" of horn or better, one might naively assume that we would get offspring that would all have 60" of horn or better at maturity. But, it obviously isn't that simple, or everyone would have cattle that rivaled the longest-horned cattle in the breed! If the heritability of horn length were 1, then we could expect that result, and the mean horn-length of the offspring would be equal to that of their parents (in this case, 61"). However, heritability of quantitative traits is almost always much lower than 1, and usually much less than 0.5. Let's assume that heritability of horns is around 0.2. In that case, the response we would expect to the selection we imposed (or in other words, the change in the mean of the trait in a population after selection, R), would (from the breeder's equation) be equal to

R = 0.2 (9") = 1.8"

In other words, we would expect the mean horn length of the offspring to be 53.8" at maturity (an increase in mean horn length of 1.8" in just one generation of selection). The upper end (the longest horned cows and bulls) would also likely shift upwards. Note that the degree of change is due to two factors: R is the product of the heritability of the trait and the degree of selection. If heritability is higher, then the response would also be proportionally higher; if the degree of selection is lower, then the response would also be proportionally lower.

In a randomly-mating population, heritability may be estimated by calculating the slope of a regression of offspring against the mid-point of the two parents. If we simply re-arrange the breeder's equation, we get:

R/ S = h²

In a regression of offspring on the mid-point of the two parents, R, S, and h² may be represented graphically like this:

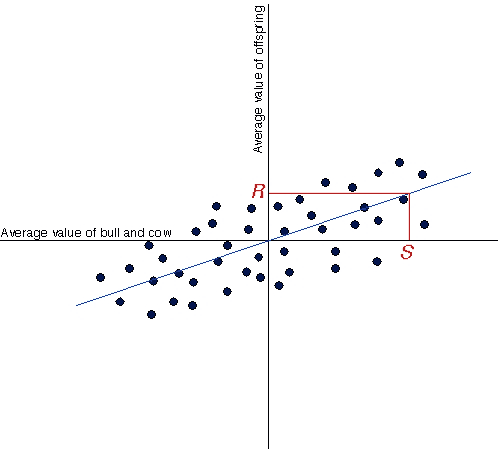
In this figure, the value of the slope of the regression line is an estimate of h², and for any mid-value of parents (S), we can predict the average expectation for their offspring (R). If heritability is low (i.e., the slope of the line is relatively flat), then we can expect only a small response in the offspring. If heritability is very high (i.e., the slope of the line is close to 1), then we would expect the offspring to express very similar values (on average) to the mid-point of the trait in the two parents.

Heritability has been measured for many traits in cattle, but to my knowledge there are not yet any studies that have estimated and reported heritability of horn length in Texas Longhorns (if anyone has the appropriate records, I'd be interested in calculating it; if anyone knows of any estimates, please e-mail me). Clearly, there has been a considerable increase in average horn length in Texas Longhorns over the past four decades in response to fairly intense selection. In the 1960s and early 1970s, Texas Longhorns with horns >40" tip-to-tip were considered exceptional. Today, a mature 40" Texas Longhorn cow is considered to have short horns, and the benchmarks have moved up to 60", 70", or even 80" in some elite circles. That's an increase of almost 1" per year.

Although the definitive study of heritability of horn length in Texas Longhorns has not yet been carried out, many other traits of interest have been studied. For instance, there have been numerous studies of heritability of milk production in cattle, with estimates of heritability ranging from about 0.20–0.35. The fat content of milk has an even higher heritability (0.4–0.5). Scrotal circumference of bulls also has high heritability (0.48), as does mature cow weight (0.5). Many traits that measure the quantity and quality of meat also have relatively high heritabilities (e.g., lean yield: 0.5; fat thickness: 0.45; longissimus muscle area: 0.4), as do several traits associated with health, fitness, and behavior (horn fly resistance: 0.6; pulmonary arterial pressure: 0.4; disposition: 0.4). Subjective sensory traits of meat tend to have lower heritability scores (e.g., tenderness: 0.22; flavor intensity: 0.1; overall acceptability: 0.04), although there is also greater variation in heritability estimates across studies for these latter traits.

Some breeding programs of Texas Longhorns today emphasize horn length over all other traits. Although this will produce some very long-horned cows and bulls in the short term, there is also a potential danger in this approach. Given the high heritability of many other traits such as milk production, mature weight, disease resistance, and disposition, and the low or even negative correlation between horn length and some other desirable traits, a program that selects only on horn length will almost certainly suffer in overall quality in the long term. There is nothing wrong with selecting for long horns (especially since horn length seems to dominate Texas Longhorn pricing these days), but care should be made to select for all the other traits that make Texas Longhorns unique and valuable, as well. The longest-horned cow in the breed won't be of much use if she produces too little milk to raise a healthy calf, or if she doesn't calve until she is five years old, or if she only produces a calf every third year, or if she is highly susceptible to disease or parasites. These extremes may seem unlikely now, but the Texas Longhorn breed clearly has the ability to change quickly in response to artificial (as well as natural) selection. So go ahead and breed for long horns (if that is your interest), but also take care to select your bulls and cows for the other traits that make Texas Longhorns unique and valuable. Otherwise, we could end up destroying the breed that we are trying to save and promote.